Banco de Questões - SAEB/Matemática Ensino Fundamental

ENSINO FUNDAMENTAL - ANOS FINAIS

Geometrias

Fonte: Secretaria de Estado da Educação - Paraná

1. O mapa a seguir mostra algumas ruas do centro de uma cidade qualquer.

Identifique as coordenadas para localizar no mapa a Praça do Sol:

a) A5

b) E5

c) F3

d) G10

2. O desenho a seguir apresenta o mapeamento das carteiras dos alunos em uma sala de aula. Observe o desenho e assinale a alternativa correta.

a) Paulo está sentado na terceira carteira da 2ª fila.

b) Lucia está sentada três carteiras antes de Michele.

c) Cleuza está na 3ª fila sentada duas carteiras antes de Davi.

d) Davi está na 4ª fila e Adriano está sentado ao seu lado na 5ª fila.

3. Solange e João estavam caminhando no Parque Central de sua cidade, conforme o mapa a seguir:

Em relação ao Parque Central, João segue a Avenida Leste-Oeste por 1 quadra na direção oeste e 3 quadras na direção norte, já Solange segue 2 quadras pela Avenida na direção leste e 3 quadras na direção sul. Em quais estabelecimentos eles chegaram, respectivamente?

a) Supermercado e Hospital.

b) Escola e Centro Comercial.

c) Hospital e Banco.

d) Banco e Escola

4. Este é o mapa de um bairro cujos quarteirões são quadrados de 100 m de lado:

A afirmação falsa é:

a) Para ir de carro de A até B percorreu-se no mínimo 400 km

b) A rua João não é perpendicular à rua Luís

c) A rua Clara e a rua Ana são perpendiculares

d) A rua Rui e a rua Oto são paralelas

5. Observe as figuras a seguir:

Estas figuras correspondem, respectivamente a:

a) Uma pirâmide de base triangular e a um prisma de base retangular.

b) Uma pirâmide de base quadrada e a um prisma de base hexagonal.

c) Um prisma de base quadrada e a uma pirâmide de base hexagonal.

d) Um prisma de base triangular e uma pirâmide de base retangular.

6. Comparando os ângulos das figuras a seguir, pode-se dizer que os triângulos são:

a) congruentes.

b) eqüiláteros.

c) isósceles.

d) retângulos.

7. Observe os triângulos apresentados na sequência:

Indique uma característica presente em todas as figuras apresentadas.

a) Os triângulos possuem um ângulo maior que 90 graus.

b) Os triângulos possuem um ângulo reto. 18Matemática – Anos Finais do Ensino Fundamental - Prova Brasil - 2009

c) Os ângulos são menores que 90 graus.

d) Não apresentam características comuns.

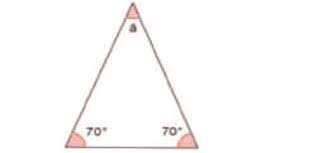
8. Ao arrumar a mesa para o jantar, Paula dobrou o guardanapo em forma de um triângulo isósceles. Qual é a medida do ângulo â?

a) â = 20°

b) â = 40°

c) â = 70°

d) â = 140°

9. Marina está confeccionando uma caixa para colocar um presente para sua mãe. Como ela quer uma caixa bem original, desenhou no papel a base para o fundo da sua caixa. O desenho tem a forma de um quadrilátero com todos os lados com a mesma medida, dois ângulos agudos e dois obtusos. Qual o quadrilátero que será utilizado por Marina para confeccionar a caixa?

a) trapézio isósceles.

b) losango.

c) trapézio retângulo.

d) retângulo.

10. Paulo está confeccionando um papagaio de papel para uma competição que acontecerá em sua cidade no final de semana, conforme desenho abaixo. Para impressionar, Paulo deseja confeccionar um papagaio que tenha dimensões cinco vezes maiores que o de seu papagaio atual. Para isso ele deve:

a) dividir as dimensões do papagaio atual por 5.
b) multiplicar as dimensões do papagaio atual por 5.
c) multiplicar as dimensões do papagaio atual por 2.
d) dividir as dimensões do papagaio atual por 2.

11. Quantos graus percorrem o ponteiro dos minutos de um relógio em 20 minutos?

a) 90º

b) 120º

c) 124º

d) 135º

12. Claudia pretende fazer um pôster de uma foto para colocar em seu quarto. As medidas da foto que pretende ampliar são 9 cm x 12 cm. Como ficarão as medidas do lado do pôster, se a foto original for ampliada 4 vezes?

a) Os lados do pôster terão 4 cm a mais que a foto original.

b) Os lados do pôster terão seus lados divididos por 4.

c) Apenas uma das medidas dos lados será multiplicada por 4.

d) As medidas dos lados serão multiplicadas por 4.

13. Um artesão está confeccionando caixas de madeira para vender. Entre os formatos escolhidos para as caixas, está um pentágono regular. Sabendo que a soma dos ângulos internos desse polígono mede 540o , para confeccionar a caixa, quanto deve medir cada ângulo interno?

a) 90º

b) 108º

c) 120 º

d) 144º

14. Pedro comprou ingressos para o cinema e sentou na poltrona (J; 9). No esquema abaixo, estão localizados pontos que representam algumas poltronas no cinema. Qual deles representa a poltrona escolhida por Pedro?

a) K
b) P
c) W
d) Z

15. Cada um dos círculos a seguir, possui raio de 4 cm. A altura e a largura da pilha, respectivamente, medem:

a) 8 cm e 16 cm.

b) 16cm e 8 cm.

c) 16cm e 32 cm.

d) 32cm e 16 cm.

16. Quantos metros de fio são necessários para ligar a ponta de um poste de 8m de altura até a entrada de energia elétrica de uma casa, localizada em uma caixa que fica a 2m do solo, distante 8m do poste?
a) 4m

b) 6m

c) 8m

d) 10m

17. Observe o esquema a seguir com a localização de uma escola e um Supermercado.

Se, nesse esquema, o supermercado pode ser indicado pelo ponto (1, A), então a escola pode ser indicada pelo ponto:

a) (1; C)

b) (C; 10)

c) (3; C)

d) (C; 3)

18. O gráfico mostra duas retas no plano cartesiano, uma na cor azul e outra na cor vermelha. Analise os dados e indique qual das opções apresentadas está correta.

a) Na reta vermelha, quando x = -2, o correspondente no eixo y = 0.

b) Na reta azul, quando x = -1, o correspondente no eixo y = -1.

c) Na reta azul, quando x = 1, o correspondente no eixo y = 1.

d) Na reta vermelha, quando x = 2, o correspondente y = 0.

Grandezas e Medidas

19. Observe o mapa a seguir que apresenta um trecho de uma ciclovia na capital do Paraná.

Cada quadra tem o comprimento de 100 m. A linha verde representa a ciclovia, se um ciclista percorrer duas vezes todo esse trecho vai andar:

a) 300 m

b) 400 m

c) 800 m

d) 1 600 m

20. Uma piscina quadrada foi construída num terreno retangular, conforme figura a seguir: O proprietário deseja gramar todo o terreno em volta da piscina. Calcule quanto ele vai gastar sabendo-se que o 1m² de grama custa R$ 5,60.

a) R$ 89,60

b) R$ 358,40

c) R$ 448,00

d) R$ 537,60

21. A figura a seguir, representa um terreno em forma de trapézio e o proprietário do terreno pretende cercá-lo com uma tela. Quantos metros de tela serão necessários?

a) 96 metros

b) 104 metros

c) 124 metros

d) 128 metros

22. Um pedreiro precisa concretar uma laje de formato retangular, com dimensões 4 m por 6 m, e espessura igual a 0,1 m. Qual o volume de concreto necessário?

a) 2,4 m³

b) 2,6 m³

c) 2,7m³

d) 3,4 m³

23. Cubo representado na figura a seguir foi montado com 8 cubinhos iguais. 26Matemática – Anos Finais do Ensino Fundamental. Quantos cubinhos devem ser acrescentados para formar um outro cubo maior contendo 27 cubinhos?

a) 4

b) 8

c) 12

d) 19

24. O sólido da figura é composto por dois blocos retangulares. Qual é o volume do sólido?

a) 17050 cm³

b) 17150 cm³

c) 18250 cm³

d) 18750 cm³

25. Uma balconista vendeu 70 centímetros de tecido a um freguês. Essa balconista preencheu corretamente a nota fiscal, escrevendo:

a) 0,07 m

b) 0,070 m

c) 0,070 cm

d) 0,70 m

26. Numa sacola estão 3 kg de batata, 750 g de feijão, 400 g de queijo, 250 g de azeitona e 500 g de arroz. Qual é o peso total dos alimentos?

a) 1,9 kg

b) 3,85 kg

c) 4,75 kg

d) 4,9 kg

Números e Álgebra

27. Considerando que na reta numérica abaixo o ponto K corresponde ao número inteiro 5 e o ponto D ao número inteiro -2, indique o ponto correspondente ao número inteiro um.

a) ponto E

b) ponto G

c) ponto B

d) ponto J

28. Observe a reta a seguir, na qual as letras representam números inteiros. Dada a sequência ( 3; 4; - 2; - 4 ), assinale a sequência de letras correspondente:

a) B, C, G, E

b) B, C, F, H

c) C, B, F, H

d) C, B, G, E

29. Na reta numérica a seguir, um dos números localizado entre o –2 e – 1 pode ser:

a) – 1/5

b) 5/4

c) 9/5

d) – 5/4

30. Qual é o resultado da expressão dada pelo triplo do quadrado de -5, somando com a quarta potência de -3 e menos o dobro de 6?
a) - 168

b) - 24

c) 144

d) 294

31. Paguei R$ 74,00 por uma bolsa e uma sandália. A bolsa foi R$ 23,00 mais barata do que a sandália. Qual o preço da sandália?

a) R$ 23,00

b) R$ 25,50

c) R$ 45,50

d) R$ 48,50

32. Em um dia de inverno foi registrada ao meio-dia, em uma cidade, a temperatura de 10º C. Passadas algumas horas, nesse mesmo dia, a temperatura na cidade diminui 15º C, assim os termômetros passaram a registrar:

a) -10º C

b) - 5º C

c) 5º C

d) 25º C

33. No inverno os termômetros registraram, à tarde, a temperatura de 6°C acima de zero. Sabendo que durante a noite a temperatura baixou 7,5°C, a temperatura registrada pelos termômetros, nessa noite foi de:

a) - 13,5°C

b) - 1,5°C

c) 1,5°C

d) 13,5°C

34. Bianca e suas amigas saíram para comer uma pizza. Depois de 20 minutos de conversa elas já haviam comido 50 % da pizza. Qual fração abaixo representa o total da pizza que elas já comeram?

a) 2/4

b) 5/4

c) 3/8

d) 4/2

35. Marcos é vendedor em uma loja de bonés. No final do mês, ao verificar as vendas da loja, percebeu que, de um total de 25 bonés, havia vendido 12. Qual a fração que representa o número de bonés que ficaram no estoque?

a)12/25

b) 9/25

c) 13/25

d) 1/25

36. Regina, Bruno, Carlos e Mariana participaram de uma olimpíada de Matemática. Do total das questões propostas Regina acertou 2/5 , Bruno acertou 1/2 , Carlos acertou 3/8 e Mariana acertou 2/4. Houve um empate entre dois deles. Identifique os dois participantes que acertaram o mesmo número de questões.

a) Regina e Bruno

b) Bruno e Carlos

c) Carlos e Mariana

d) Bruno e Mariana

37. Pensando em modernizar sua casa, uma arquiteta desenhou uma faixa na parede de seu quarto, como mostra a figura abaixo, que será pintada de azul e rosa. Até o momento, o pintor só utilizou a tinta azul. A fração que representa a parte pintada da faixa é igual a:

a) 2/4

b) 5/4

c) 3/8

d) 4/2

38. Paulo e Roberto têm, juntos, R$ 340,00. Paulo comprou ingresso para o jogo de futebol com 1/5 do que possuía. Roberto gastou 2/3 do que possuía na compra de ingresso para um show de música. Efetuadas essas despesas, eles ficaram com quantias iguais. Nesse caso, podemos afirmar que:

a) Paulo tinha R$ 140,00 a mais que Roberto.

b) Roberto tinha menos que o dobro da quantia de dinheiro que Paulo.

c) Paulo tinha R$ 100,00 a menos que Roberto.

d) Roberto tinha o dobro de Paulo mais R$ 40,00.

39. Júnior estava participando de uma maratona. O percurso total da prova é de 42,195 Km. Sabendo-se que ainda faltam 16,4 Km para ele completar a prova, qual a distância já percorrida por Júnior?

a) 25,920 Km

b) 25,795 Km

c) 23,795 Km

d) 40,555 Km

40. Com um total de 3,695 Km de extensão e obedecendo aos mais rígidos conceitos relativos à segurança, à funcionalidade e à qualidade, o Autódromo Internacional de Curitiba se apresenta como referência para o novo milênio. A figura a seguir mostra o desenho da pista do autódromo Internacional. O texto traz informações sobre a extensão da pista do autódromo. Podemos dizer que essa extensão corresponde a:

a) 3 km + 695 centésimos do quilômetro.

b) 3 km + 695 milésimos do quilômetro.

c) 3 km + 695 décimos do quilômetro.

d) 3 km + 695 milionésimos do quilômetro.

41. No mês de setembro, o saldo bancário de Joana era de R$ 115,00. Durante o mês ela pagou duas dívidas utilizando dois cheques, um no valor de R$ 126,50 e outro no valor de R$ 23,00. Qual o saldo de Joana no final desse mês?

a) - R$149,50

b) - R$ 34,50

c) R$ 34,50

d) R$ 149,50

42. Pedro foi ao banco, retirou um extrato de sua conta e notou que estava com um saldo negativo de R$ 356,00. Sabendo que serão debitados em sua conta dois cheques, sendo um de R$ 53,50 e outro de R$ 85,00, quanto Pedro precisa depositar para deixar a conta com um saldo positivo de R$ 30,00?

a) R$ 187,50

b) R$ 217,50

c) R$ 247,50

d) R$ 524,50

43. A capacidade do tanque de gasolina do carro de João é de 50 litros. As figuras mostram o medidor de gasolina do carro no momento de partida e no momento de chegada de uma viagem feita por João. Quantos litros de gasolina ele gastou na viagem?

a) 12,5

b) 25

c) 37,5

d) 50

44. De acordo com a tabela a seguir, marque a resposta correta:

Segundo a tabela, podemos afirmar que:

a) A área do Brasil é 2,6 vezes menor que a área da Índia.

b) A população da Índia é 16,25 vezes maior que a do Brasil.

c) A densidade demográfica do Brasil é menor que o da Índia porque sua área é menor.

d) A população da Índia é 6,25 vezes maior que a do Brasil.

45. Em um concurso estão inscritos 275 candidatos dos quais 176 são homens. A taxa percentual de mulheres é de:

a) 36

b) 56

c) 64

d) 99

46. Marcos participou de uma olimpíada de matemática da escola. Ele acertou 72% das 150 questões. O número de questões que ele errou foi de:

a) 28

b) 42

c) 78

d) 108

47. Se o salário de Antônio passou de R$ 700,00 para R$ 850,00 num período em que a inflação mensal foi de 4%, então, o reajuste foi:

a) Abaixo da inflação.

b) Acima da inflação.

c) Igual à inflação.

d) Não é possível de se calcular.

48. Márcia faz doces para vender e sua última encomenda para uma festa de aniversário de criança foi de 400 brigadeiros. Para obter essa quantidade ela usou cinco latas de leite condensado. Agora, ela recebeu uma encomenda de 720 brigadeiros. Para fazer essa quantidade, ela gastará:

a) 6 latas de leite condensado.

b) 7 latas de leite condensado.

c) 8 latas de leite condensado.

d) 9 latas de leite condensado.

49. O consumo de determinadas frutas é benéfico à saúde. Um exemplo é a pera, cujo consumo auxilia na circulação do sangue, no controle da pressão arterial e facilita a digestão. Cada 100g dessa fruta equivale a 56 calorias. Uma pessoa que ingere 450g dessa fruta, fornece ao organismo:

a) 156 calorias

b) 252 calorias

c) 468 calorias

d) 504 calorias

50. André vai realizar uma viagem em seu estado. Conforme é apresentado no mapa a seguir, a distância de Ijuí – Porto Alegre é de 2 cm aproximadamente. Veja qual é a escala do mapa e descubra a distância real aproximada entre as duas cidades.

a) 20 Km

b) 40 Km

c) 200 Km

d) 400 Km

51. Um carro percorre 5 km, enquanto no mesmo intervalo de tempo um homem caminha 40 m. Observando a razão entre os espaços percorridos pelo carro e pelo homem, concluímos que:

a) o carro percorre 125 m enquanto o homem percorre 1 m.

b) o carro percorre 5 000 m enquanto o homem percorre 4 m.

c) o carro percorre 500 m enquanto o homem percorre 40 m.

d) o carro percorre 1 250 m enquanto o homem percorre 1 m.

52. Em uma cidade do Paraná, a corrida de táxi é cobrada da seguinte maneira: R$ 3,50 de bandeirada (valor inicial mínimo estipulado para uma corrida), mais R$ 1,60 por quilômetro rodado. A fórmula que expressa o valor C da corrida em X quilômetros é: C = 3,50 + 1,60 X. Qual o valor que uma pessoa pagará por uma corrida de 13 Km?

a) R$ 5,10

b) R$ 20,08

c) R$ 23,50

d) R$ 24,30

53. O nível N de óleo de um reservatório varia com o tempo t, contado em horas, conforme a equação: N = t2 + 5t – 24 = 0. Em quanto tempo o nível de óleo chegará a zero?

a) 3 horas

b) 4 horas

c) 5 horas

d) 8 horas

54. O valor pago por uma corrida de táxi em uma cidade é dado pela equação P=5+1,5K, onde R$ 5,00 é uma quantia fixa correspondente a chamada bandeirada, e R$ 1,50 por quilômetro percorrido K. Se uma pessoa ao final da corrida pagou R$ 50,00, quantos quilômetros percorreu o táxi?

a) 20km

b) 30km

c) 35km

d) 40km

55. Com o dinheiro que economizou de sua mesada, Márcia pretende comprar um MP4 e um tênis que custa R$ 154,00. A soma do dobro do preço do MP4 com o preço do tênis é R$ 334,00. A expressão que representa esse problema é:

a) 334 – x = 154

b) 2x – 154 = 334

c) x + 2 x = 154 + 334

d) 2x + 154 = 334

56. Observe a figura a seguir: com quatro palitos podemos fazer um quadrado; com sete palitos, podemos formar uma fileira com dois quadrados e com dez palitos, uma fileira com três quadrados, e assim sucessivamente. Indique a expressão que representa o número de palitos necessários para se formar uma fileira com n palitos.

a) 2n + 2

b) 2n + 3

c) 3n + 1

d) 3n + 2 3

57. Na situação a seguir, indique a equação que nos permite encontrar o número procurado. Amanda vai realizar uma viagem e estava com 81 reais, gastou 9 reais com um almoço durante a viagem e comprou 6 refrigerantes e 6 salgados que custaram o mesmo valor cada um, para consumir durante a viajem. Qual a equação que melhor expressa o problema?

a) 6x - 9 = 81

b) 6x + 9 - 81 = 0

c) 12x = 81 + 9

d) 12x + 9 = 81

58. A expressão representa a compra de camisetas feita por uma loja na qual obteve R$100,00 de desconto: C = 15a + 10b + 18c + 12d - 100 Os preços das quatro marcas de camisetas são dados na tabela a seguir, então o valor dessa compra com o desconto foi de:

a) R$ 511,00

b) R$ 611,00

c) R$ 621,00

d) R$ 711,00

59. Observe a seqüência de figuras e identifique qual é a expressão algébrica que representa a seqüência da quantidade de quadradinhos, onde cada lado é representado por n.

a) n²

b) n² +42

c) n² +(n+1)²

d) (n+2)²

60. No início de uma festa, tinham 200 jovens. Depois o número de rapazes dobrou e o de moças aumentou 40. Com isso o número de rapazes ficou o mesmo que o de moças. Quantos rapazes e quantas moças havia no início da festa?

a) 80 rapazes e 120 moças.

b) 120 rapazes e 80 moças.

c) 160 rapazes e 120 moças.

d) 160 rapazes e 160 moças.

61. Na lanchonete de uma escola o preço do salgado é R$ 2,00 e o preço do sanduíche é R$ 3,00, que são os lanches vendidos. Em uma manhã foram vendidos 70 lanches. O valor arrecadado em todo o dia foi de R$ 180,00. Qual sistema a seguir representa o problema?

a) x + y = 70

2x + y = 180

b) x + 3y = 50

2x + y = 180

c) x + y = 70

2x + 3y = 180

d) 2x + 3y = 70

x + y = 180

62. Em uma garagem há carros e motos totalizando 30 veículos. O administrador da garagem abaixou-se e contou 82 pneus. Com isso, o administrador concluiu que na garagem há:

a) 19 motos e 11 carros.

b) 10 carros e 20 motos.

c) 11 carros e 19 motos.

d) 12 carros e 18 motos.

63. Observe o gráfico a seguir: Esse gráfico é a solução (representação geométrica) do sistema:

a) x + y = 12

x – y = 2

b) x + y = 7

2x + 4y = 22

c) x + y = 7

2x – y = - 1

d) x + 2y = 5

2x + y = - 2

64. Observe o gráfico a seguir e indique a solução do sistema que representa o gráfico:

a) x + y = 4

x – y = 2

b) x + y = 4

x – y = 4

c) x + 2y = 4

x – 2y = 2

d) x + 2y = 4

2y = 2

65. Os sistemas de equações apresentam uma interpretação gráfica. Indique o gráfico que melhor representa o sistema a seguir:

x + y = 2

x – y = 0

66. A velocidade de um automóvel varia com a aceleração constante em função do tempo, obedecendo a seguinte equação v = 10 + 2.t. O gráfico que melhor representa a equação anterior é :

Tratamento da Informação

67. A tabela a seguir traz a população dos cinco municípios mais populosos do Paraná:

Ao observar os dados da tabela, podemos afirmar que:

a) A soma da população dos municípios B, C, D e E é maior que a de Curitiba.

b) Curitiba tem aproximadamente o triplo de habitantes de Ponta Grossa e Foz do Iguaçu.

c) Foz do Iguaçu tem mais do que o dobro da população de Londrina.

d) A diferença da população de Curitiba e Maringá é de 1 milhão de habitantes.

68. Em uma pesquisa onde 2 673 pessoas foram entrevistadas com o seguinte questionamento: O que leva as pessoas a se mudarem para os condomínios fechados fora das grandes cidades?

As respostas foram organizadas no gráfico a seguir, após análise do gráfico, pode-se afirmar que, aproximadamente:

a) 321 pessoas mudam devido ao conforto.

b) 588 pessoas mudam devido à tranquilidade.

c) 749 pessoas mudam devido ao espaço.

d) 1 016 pessoas mudam devido à segurança.

69. A professora Lisiane de Matemática realizou um levantamento para saber a preferência musical dos alunos das 7ª séries A e B. O gráfico seguinte mostra o resultado obtido por ela:

Com base no gráfico anterior é possível dizer que:

a) O estilo musical preferido pela maioria dos alunos é Hip Hop.

b) A maioria dos alunos prefere Sertaneja.

c) O estilo musical preferido pela maioria dos alunos é Pop.

d) O estilo musical menos ouvido é MPB.

70. O gráfico a seguir mostra os resultados de jogos na Copa de 2006. De acordo com o gráfico é correto afirmar que:

a) O Brasil marcou 7 gols.

b) A média de gols marcados pelo Brasil foi de 2 gols por jogo.

c) 2% dos gols foram marcados contra a Holanda (HOL).

d) O Brasil marcou mais gols contra a Camarões (CAM) do que contra a Itália (ITA).

71. O gráfico a seguir apresenta as vendas de equipamentos agrícolas de uma indústria:

Pode-se afirmar que:

a) foram vendidos 90 equipamentos até abril.

b) as vendas aumentaram mês a mês.

c) foram vendidos 100 equipamentos até junho.

d) o faturamento da indústria aumentou de março para abril.

72. A tabela a seguir mostra os rendimentos mensais com as respectivas alíquotas e deduções do imposto de renda – I.R.

Neste período, o salário mensal de Renata era de R$ 2 500,00, então:

a) Renata era isenta.

b) Renata deve pagar R$ 375,00 de I. R.

c) Renata deve pagar R$ 495,00 de I. R.

d) Renata deve pagar R$ 687,50 de I. R.

GABARITO

1 c

2 d

3 d

4 c

5 b

6 a

7 b

8 b

9 b

10 b

11 b

12 d

13 b

14 a

15 c

16 d

17 c

18 b

19 d

20 c

21 b

22 a

23 d

24 d

25 d

26 d

27 b

28 b

29 d

30 d

31 d

32 b

33 b

34 a

35 c

36 d

37 a

38 d

39 b

40 b

41 b

42 d

43 b

44 d

45 a

46 b

47 b

48 d

49 b

50 d

51 a

52 d

53 a

54 b

55 d

56 c

57 d

58 a

59 a

60 a

61 c

62 c

63 b

64 a

65 b

66 b

67 b

68 d

69 c

70 b

71 a

72 d

ENSINO MÉDIO

Fonte: Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira

1. Um copo cilíndrico, com 4 cm de raio e 12 cm de altura, está com água até a altura de 8 cm. Foram então colocadas em seu interior n bolas de gude, e o nível da água atingiu a boca do copo, sem derramamento. Qual é o volume, em cm³ , de todas as n bolas de gude juntas?
(A) 32π
(B) 48π
(C) 64π
(D) 80π
(E) 96π

2. Em uma escola, há 400 estudantes do sexo masculino e 800 do sexo feminino. Escolhendo-se ao acaso um estudante dessa escola, qual a probabilidade de ele ser do sexo feminino?

(A) 1/4

(B) 1/3

(D) 1/2

(E) 2/3

3.Uma lata de leite em pó, em forma de um cilindro reto, possui 8 cm de altura com 3 cm de raio na base. Uma outra lata de leite, de mesma altura e cujo raio é o dobro da primeira lata, possui um volume:

(A) duas vezes maior.

(B) três vezes maior.

(D) sete vezes maior.

(E) oito vezes maior.

4. Duas pessoas, partindo de um mesmo local, caminham em direções ortogonais. Uma pessoa caminhou 12 metros para o sul, a outra, 5 metros para o leste. Qual a distância que separa essas duas pessoas ?

(A) 7m

(B) 13m

(D) 60m

(E) 119m

5. Um pintor dispõe de 6 cores diferentes de tinta para pintar uma casa e precisa escolher uma cor para o interior e outra diferente para o exterior, sem fazer nenhuma mistura de tintas. De quantas maneiras diferentes essa casa pode ser pintada usando-se apenas as 6 cores de tinta que ele possui?

(A) 6

(B) 15

(D) 30

(E) 60

6. O termo que ocupa a posição n em uma progressão aritmética (PA) de razão r é dado pela fórmula an = a1 + (n - 1)r. Com o auxílio dessa informação, assinale a alternativa que apresenta o décimo quarto termo de uma PA de razão 3, cujo primeiro termo é igual a 20.

(A) 39

(B) 42

(D) 62

(E) 70

7. Ao passar sua mão direita por todos os vértices e arestas de um poliedro, somente uma vez, um deficiente visual percebe que passou por 8 vértices e 12 arestas. Conclui-se que o número de faces desse poliedro é igual a:

(A) 20

(B) 12

(D) 6

(E) 4

8. Decompondo o polinômio P(x) = 5x² + 5x – 30 em fatores do 1º grau, obtém-se:

(A) 5( x – 5) ( x – 3 )

(B) 5( x – 2) ( x + 3 )

(D) 5( x – 2 ) ( x – 3 )

(E) 5( x + 5) ( x + 3 )

9. Para alugar um carro, uma locadora cobra uma taxa básica fixa acrescida de uma taxa que varia de acordo com o número de quilômetros rodados. A tabela seguinte mostra o custo total (C) do aluguel, em reais, em função do número de quilômetros rodados (q).

Quilômetros rodados (q) Custo (C)

10 55

20 60

30 65

40 70

A sentença que representa o custo total é:

(A) C(q) = 5q + 5.

(B) C(q) = 4q + 15.

(D) C(q) = q/2 + 50.

(E) C(q) = q /10+ 55.

10. Imagine que o alojamento das equipes de vôlei masculino e feminino, nas Olimpíadas de Atenas, estão em uma mesma avenida. Como pessoas do mesmo sexo não podem ficar juntas, elas foram separados à esquerda e à direita do Centro de Apoio de Atenas (CAA), que está localizado no meio da avenida, e que está representado pelo zero. Os meninos ficam à esquerda e a localização deles é representada pelo sinal menos (–) e as meninas ficam à direita, com localização representada pelo sinal mais (+).

Qual é a localização das equipes do Brasil de vôlei masculino e feminino, respectivamente, na avenida olímpica?

(A) 45 e 55.

(B) – 45 e – 55.

(D) – 55 e 45.

(E) 45 e –55.

11. Uma pedra é largada de uma certa altura e cai em queda livre. Desprezando-se a resistência do ar, a velocidade da pedra durante a queda é expressa por v = g × t, em que g = 10 m/s² é a aceleração da gravidade e t é o tempo transcorrido, em segundos. Qual é o gráfico que melhor ilustra a velocidade da pedra em função do tempo, até o momento em que ela chega ao solo?

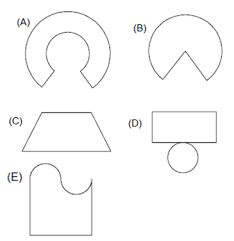
12. Ao fazer um molde de um copo, em cartolina, na forma de cilindro de base circular qual deve ser a planificação do mesmo?

13. Ao estudar um pássaro, um pesquisador utilizou um aparelho para captar seu canto. O som captado pelo pesquisador pode ser representado pelo gráfico seguinte.

Qual a função que representa esse gráfico no intervalo [0, 2π]?
(A) y = −cos x .
(B) y = cosx/2
(D) y = sen2x .

(E) y = 2 senx .

14. O gráfico seguinte mostra a distância, em metros, que um pequeno roedor está de sua toca, no período de 17h até às 23h.

Os dados indicam que o animal às 18h se encontra:

(A) mais longe da toca do que às 23h.

(B) a 10 metros mais perto da toca do que às 20h.

(D) a 16 metros mais perto da toca do que às 17h.

(E) mais longe da toca do que às 19h.

GABARITO

1 C

2 E

3 C

4 B

5 D

6 C

7 D

8 B

9 D

10 D

11 C

12 D

13 C

14 A

Pesquisar este blog

Professora Márcia Guimarães